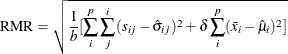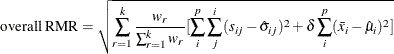Going through our archives, we came across this great post from September 2, 2014 on, “Really Teaching Statistics” that we wanted to share with you in case you missed it the first time around.
- Bar graphs
- Line plots
- X,Y coordinates
- Fractions and decimals (since the mean is rarely going to be an integer)
- Ratios and proportions – in summarizing a data set, it’s pretty common to point out, for example, that the ratio of game fish to non-game fish was 3:2. We are often asking if the percentage of something observed is disproportionate to the percentage in the population.
It doesn’t bother me that these topics are not called statistics, I’m just pointing it out. Whether a line is considered a regression line or simply points in two-dimensional space is a matter of context and nothing else.
Speaking of lines and graphs, the very basis of describing a distribution starts with graphing it. So, those second grade bar graphs? Precursors to sixth grade requirements to summarize and described a set of data.
You might say I’m going to an extreme including fractions in there because I may as well throw in addition and division. After all, you need to add up the individual scores and divide by N. Actually, I wouldn’t argue too much with that view.
You can’t even compute a standard deviation without understanding the concepts of squares and square roots, so it would be easy to argue that is at least a prerequisite to statistics.
While I’ve heard a lot of people hating on the common core, personally, I’m interested in seeing how it plays out.
What I expect will continue to happen is that many children will be turned off of math by the third grade because it is generally taught SO abysmally. That isn’t all the fault of teachers – the books they are given to use are often deathly boring. This isn’t to say I am not bothered by the situation. It bothers me a lot.
Working mostly in low-performing schools, I see students who are not very proficient with fractions, proportions, exponents or mathematical notation. We are trying to design our games to teach all of those prerequisites and then start showing students different distributions, having them collect and interpret data.
Lacking prerequisites is one of the three biggest barriers I see in teaching statistics, or any math, to students. The other two are related; low expectations for what students should be able to learn at each grade, and the fiction on the part of teachers and students that everything should be easy.
People were all up in arms years ago because there was a Barbie doll that said, “Math is hard.”
Guess what? Math is hard sometimes and that is why you have to work hard at it. Even if you really like math and do well at it in school, even if it’s your profession, there are times when you have to spend hours studying it and figuring something out.
Today, I was reviewing textbooks for a course I’ll be teaching on multivariate statistics. I didn’t like any of the three I read for the course, although I found one of them pretty interesting just from a personal perspective. The one I liked had pages after pages of equations in matrix algebra and it would be a definite stretch for most masters students. I’m really debating using it because I know, just like with the middle school students, there will be many lacking prerequisites and it will take a LOT of work on my part to explain vectors, determinants before we can even get to what they are supposed to be learning.
Last week, I had someone seriously ask me if we could make our games “look less like math so that students are learning it without realizing it”. No, we cannot. There’s nothing wrong with learning math that you need to disguise it to look like something else.
Whenever I catch myself thinking in designing a game, “Will the students be able to do X?” and I think they will not because they are lacking the prerequisites, I build an earlier level to teach the prerequisites and go ahead and include X anyway.
Here is why — I’m sitting at the other end teaching graduate students where the text begins like this:
root mean square residual (RMR) For a single-group analysis, the RMR is the root of the mean squared residuals:
where
is the number of distinct elements in the covariance matrix and in the mean vector (if modeled).
For multiple-group analysis, PROC CALIS uses the following formula for the overall RMR:
“The probability distribution (density) of a vector y denoted by f(y) is the same as the joint probability distribution of y1 …. yp . “
“It is easy to verify that the correlation coefficient matrix, R, is a symmetric positive definite matrix in which all of the diagonal elements are unity.”